Язык этой книги, как и большинства математических текстов, состоит из обычного языка и ряда специальных символов излагаемых теорий. Наряду с этими специальными символами, которые будут вводиться по мере надобности, мы используем распространенные символы математической логики для обозначения соответственно отрицания «не» и связок «или», «влечет», «равносильно».

Возьмем, например, три представляющих и самостоятельный интерес высказывания:

L. «Если обозначения удобны для открытий то поразительным образом сокращается работа мысли» Лейбниц).

Р. «Математика - это искусство называть разные вещи одинаковыми именами» (А. Пуанкаре).

G. «Великая книга природы написана языком математики» (Г. Галилей).

Тогда в соответствии с указанными обозначениями:


Мы видим, что пользоваться только формальными обозначениями, избегая разговорного языка, - не всегда разумно.

Мы замечаем, кроме того, что в записи сложных высказываний, составленных из более простых, употребляются скобки, выполняющие ту же синтаксическую функцию, что и при записи алгебраических выражений. Как и в алгебре, для экономии скобок можно договориться о «порядке действий». Условимся с этой целью о следующем порядке приоритета символов:

При таком соглашении выражение следует расшифровать как соотношение - как , но не как .

Записи , означающей, что А влечет В или, что то же самое, В следует из А, мы часто будем придавать другую словесную интерпретацию, говоря, что В есть необходимый признак или необходимое условие А и, в свою очередь, А - достаточное условие или достаточный признак В. Таким образом, соотношение А В можно прочитать любым из следующих способов:

А необходимо и достаточно для В;

А тогда и только тогда, когда В;

А, если и только если В;

А равносильно В.

Итак, запись А В означает, что А влечет В и, одновременно, В влечет А.

Употребление союза и в выражении пояснений не требует.

Следует, однако, обратить внимание на то, что в выражении союз или неразделительный, т. е. высказывание считается верным, если истинно хотя бы одно из высказываний А, В. Например, пусть х - такое

действительное число, что Тогда можно написать, что имеет место следующее соотношение:

2. Замечания о доказательствах.

Типичное математическое утверждение имеет вид , где А - посылка, заключение. Доказательство такого утверждения состоит в построении цепочки следствий, каждый элемент которой либо считается аксиомой, либо является уже доказанным утверждением

В доказательствах мы будем придерживаться классического правила вывода: если А истинно и , то В тоже истинно.

При доказательстве от противного мы будем использовать также принцип исключенного третьего, в силу которого высказывание (А или не А) считается истинным независимо от конкретного содержания высказывания А. Следовательно, мы одновременно принимаем, что , т. е. повторное отрицание равносильно исходному высказыванию.

3. Некоторые специальные обозначения.

Для удобства читателя и сокращения текста начало и конец доказательства условимся отмечать знаками соответственно.

Условимся также, когда это будет удобно, вводить определения посредством специального символа (равенство по определению), в котором двоеточие ставится со стороны определяемого объекта.

определяет левую часть посредством правой части, смысл которой предполагается известным.

Аналогично вводятся сокращенные обозначения для уже определенных выражений. Например, запись

вводит обозначение для стоящей слева суммы специального вида.

4. Заключительные замечания.

Отметим, что мы здесь говорили, по существу, только об обозначениях, не анализируя формализм логических выводов и не касаясь глубоких вопросов истинности, доказуемости, выводимости, составляющих предмет исследования математической логики.

Как же строить математический анализ, если мы не имеем формализации логики? Некоторое утешение тут может состоять в том, что мы всегда знаем или, лучше сказать, умеем больше, чем способны в данный момент формализовать. Пояснением смысла последней фразы может служить известная притча о том, что сороконожка даже ходить разучилась, когда ее попросили объяснить, как именно она управляется со всеми своими конечностями.

Опыт всех наук убеждает нас в том, что считавшееся ясным или простым и нерасчленяемым вчера может подвергнуться пересмотру или уточнению сегодня. Так было (и, без сомнения, еще будет) и с многими понятиями математического анализа, важнейшие теоремы и аппарат которого были открыты еще в XVII-XVIII веках, но приобрели современный формализованный, однозначно трактуемый и, вероятно, потому общедоступный вид лишь после создания теории пределов и необходимой для нее логически полноценной теории действительных чисел (XIX век).

Именно с этого уровня теории действительных чисел мы и начнем в главе II построение всего здания анализа.

Как уже отмечалось в предисловии, желающие быстрее ознакомиться с основными понятиями и эффективным аппаратом собственно дифференциального и интегрального исчисления могут начать сразу с III главы, возвращаясь к отдельным местам первых двух глав лишь по мере необходимости.

Упражнения

Будем отмечать истинные высказывания символом 1, а ложные - символом 0. Тогда каждому из высказываний можно сопоставить так называемую таблицу истинности, которая указывает его истинность в зависимости от истинности высказываний А, В. Эти таблицы являются формальным определением логических операций Вот они:


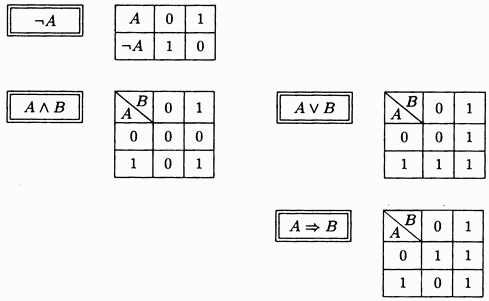
1. Проверьте, все ли в этих таблицах согласуется с вашим представлением о соответствующей логической операции. (Обратите, в частности, внимание на то, что если А ложно, то импликация всегда истинна.)

2. Покажите, что справедливы следующие простые, но очень важные и широко используемые в математических рассуждениях соотношения:

3.Введение в анализ

Символы математической логики

Для сокращения записи утверждений используются символы:

– квантор общности , означающий «для любого», «для каждого»;

– квантор существования , означающий «существует»;

! – квантор единственности , означающий «единственное»;

| – символ, означающий «при», «такое что», «имеет место»;

– знак логического следствия (запись «» означает «из утверждения A следует утверждение B »);

– знак двойного логического следствия (запись «» означает «из утверждения A следует утверждение B , и из утверждения B следует утверждение A », или «утверждения A и B эквивалентны»);

– знак логического «или» (запись «» означает «выполнено хотя бы одно из утверждений A или B »);

– знак логического «и» (запись «» означает «выполнены оба утверждения A и B »);

Вместо знака логического следствия в некоторых случаях используют близкую по смыслу запись в виде пары круглых скобок.

3.1Множества

Наиболее общим понятием математики является понятие множества. Дать определение этому понятию не удается; можно лишь пояснить, что близкими по содержанию являются такие понятия, как набор и совокупность. Подобного описания вполне достаточно, так как при построении теории природа самих объектов игнорируется: предметом исследования являются лишь свойства операций , отношений между объектами определенных множеств.

Для обозначения того, что объект a является элементом множества A , используют знак принадлежности


;

если объект a не является элементом множества A , то записывают


.

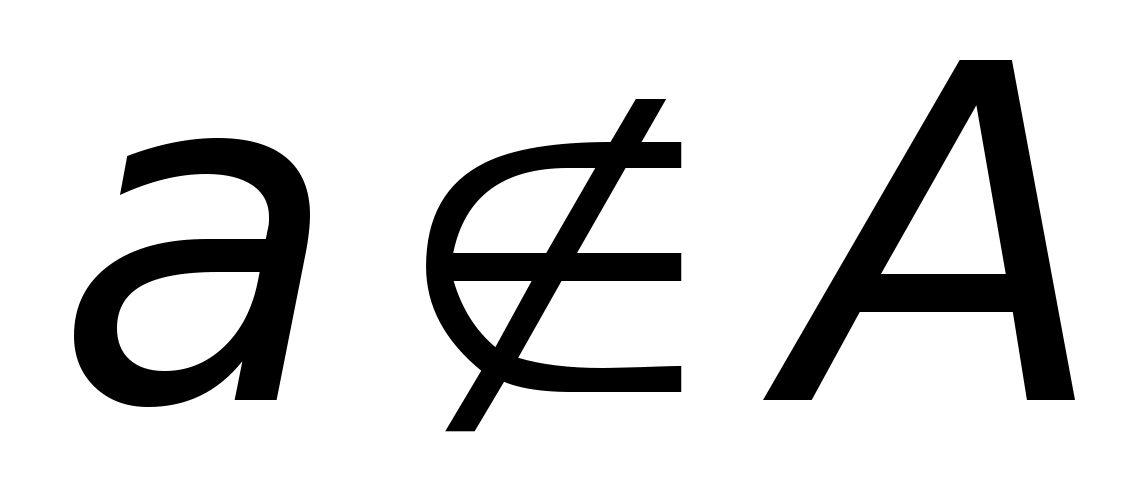Задать множество можно двумя способами. Первый способ состоит в перечислении всех элементов. Например, множество

состоит из чисел 1, 2 и 3; множество

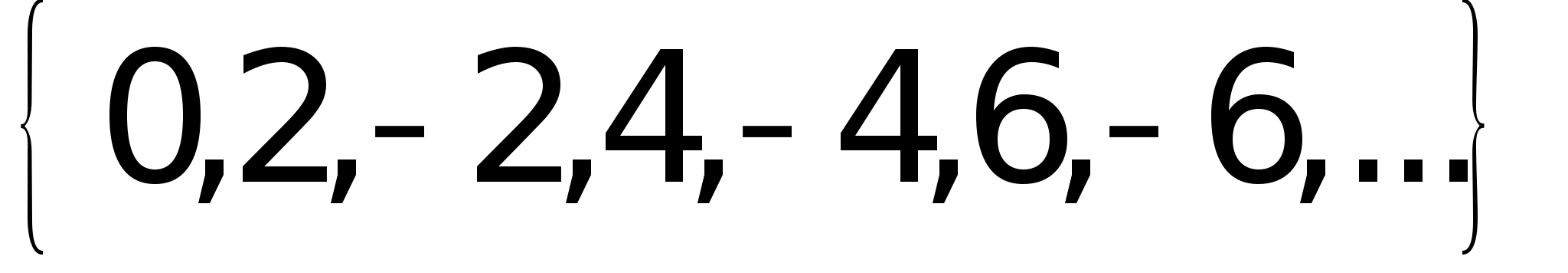состоит из всех четных чисел, и т.д.

Второй способ состоит в указании характеристического свойства, которым обладают те и только те элементы, которые принадлежат данному множеству. Например, множество всех четных чисел можно определить так:


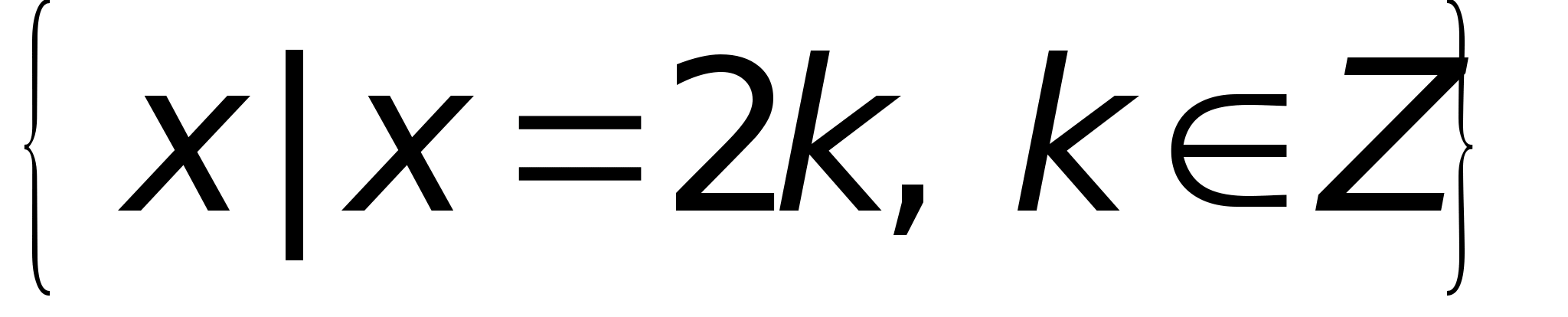
(читается «множество x , таких что

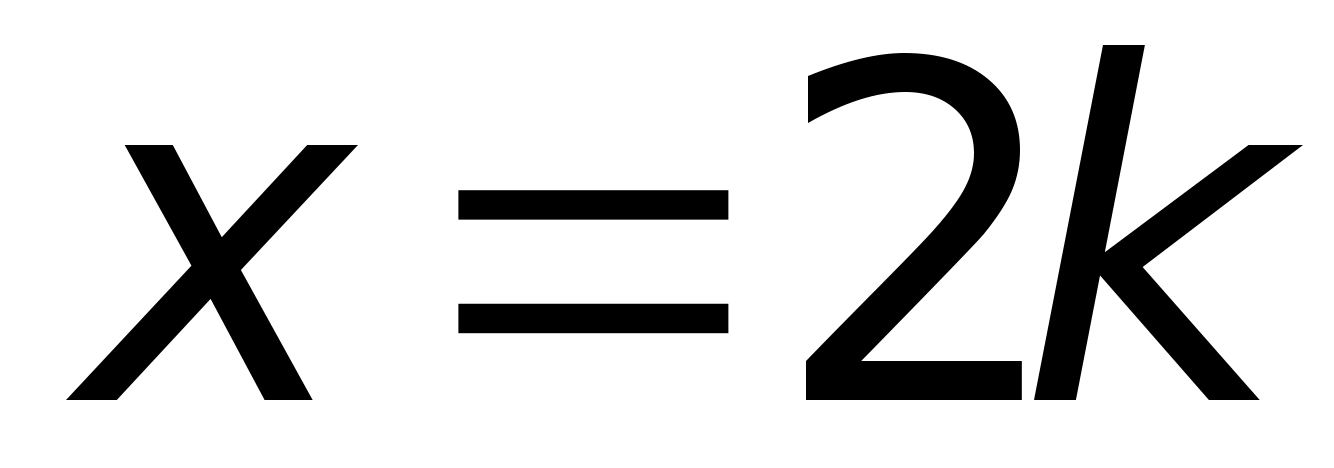»); здесь Z – множество целых чисел.

Два множества называют равными, если они состоят из одних и тех же элементов. Равенство множеств обладает такими же свойствами, что и равенство чисел:

1.

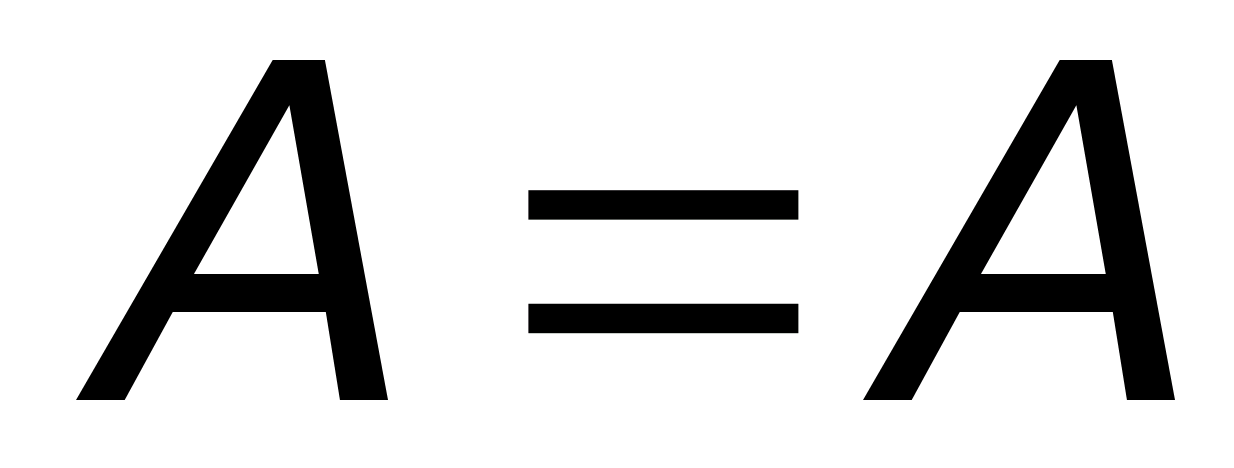(равенство рефлексивно).

2. Если

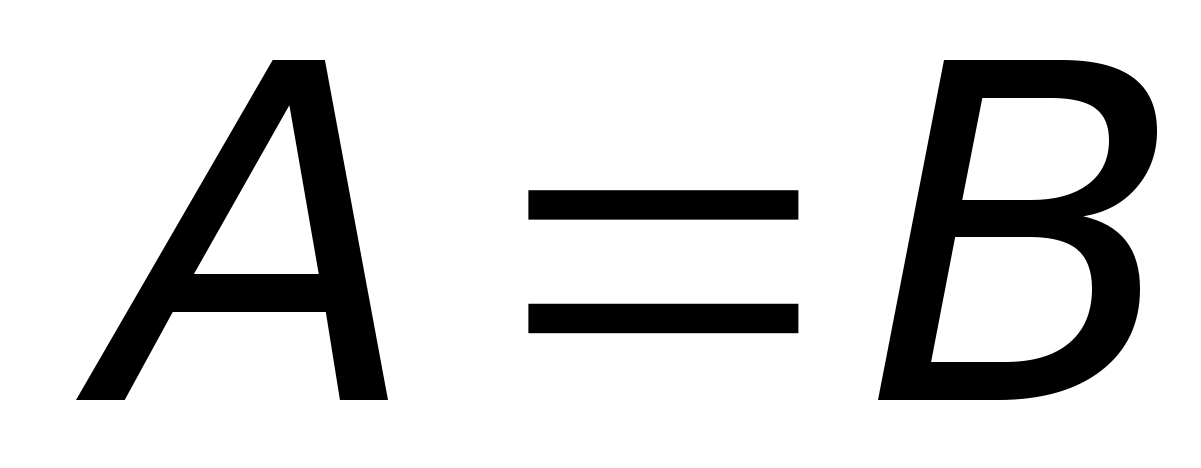то

(равенство симметрично).

3. Если и

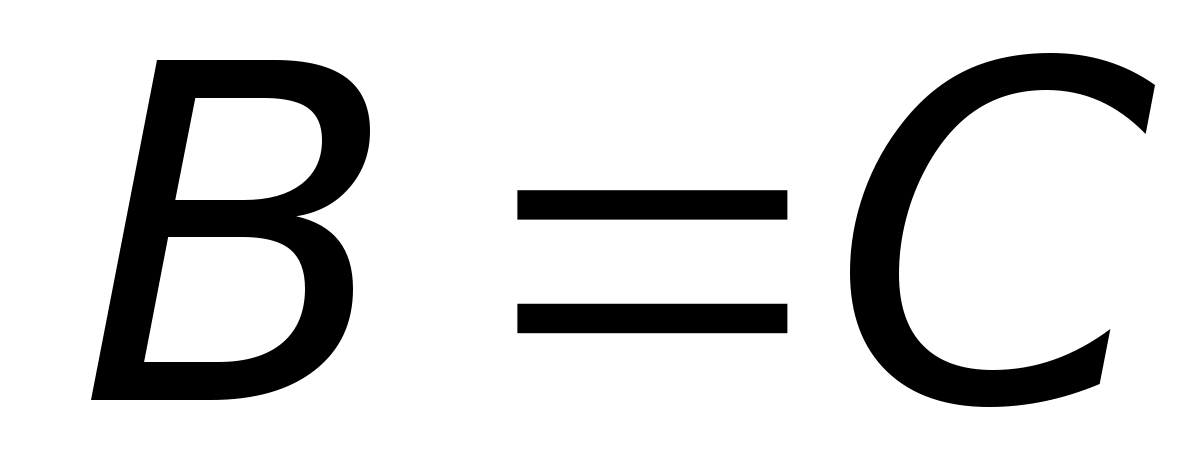то

(равенство транзитивно).

Множество A называют подмножеством множества B , если любой элемент множества A является элементом множества B . Отношение «являться подмножеством» записывают при помощи знака включения:


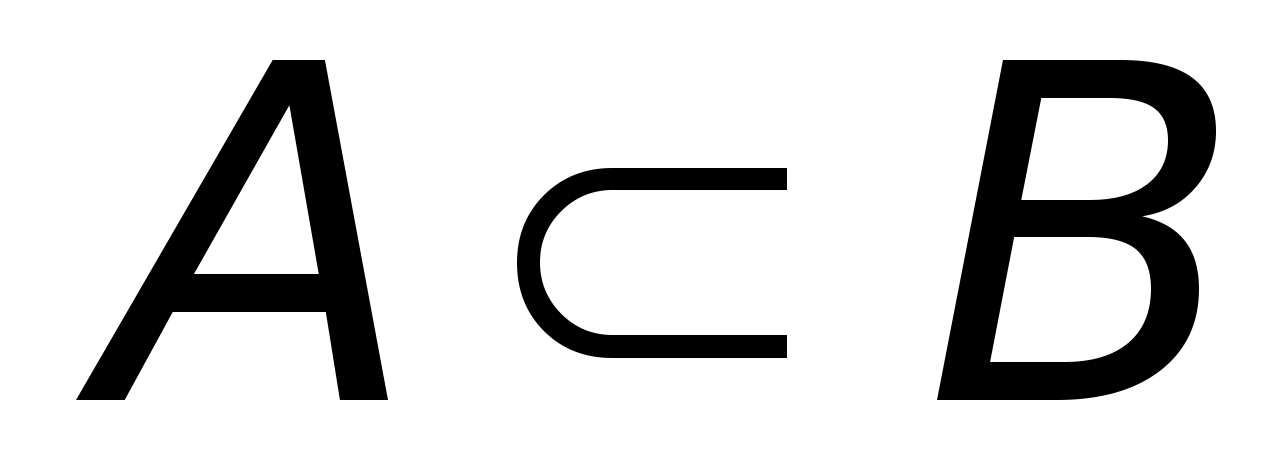
(читается «A включается в B » или «B включает A »). Если при этом множества A и B не равны, то A называют собственным подмножеством B .

Два множества A и B равны тогда и только тогда, когда A является подмножеством B и множество B является подмножеством A .

Множество

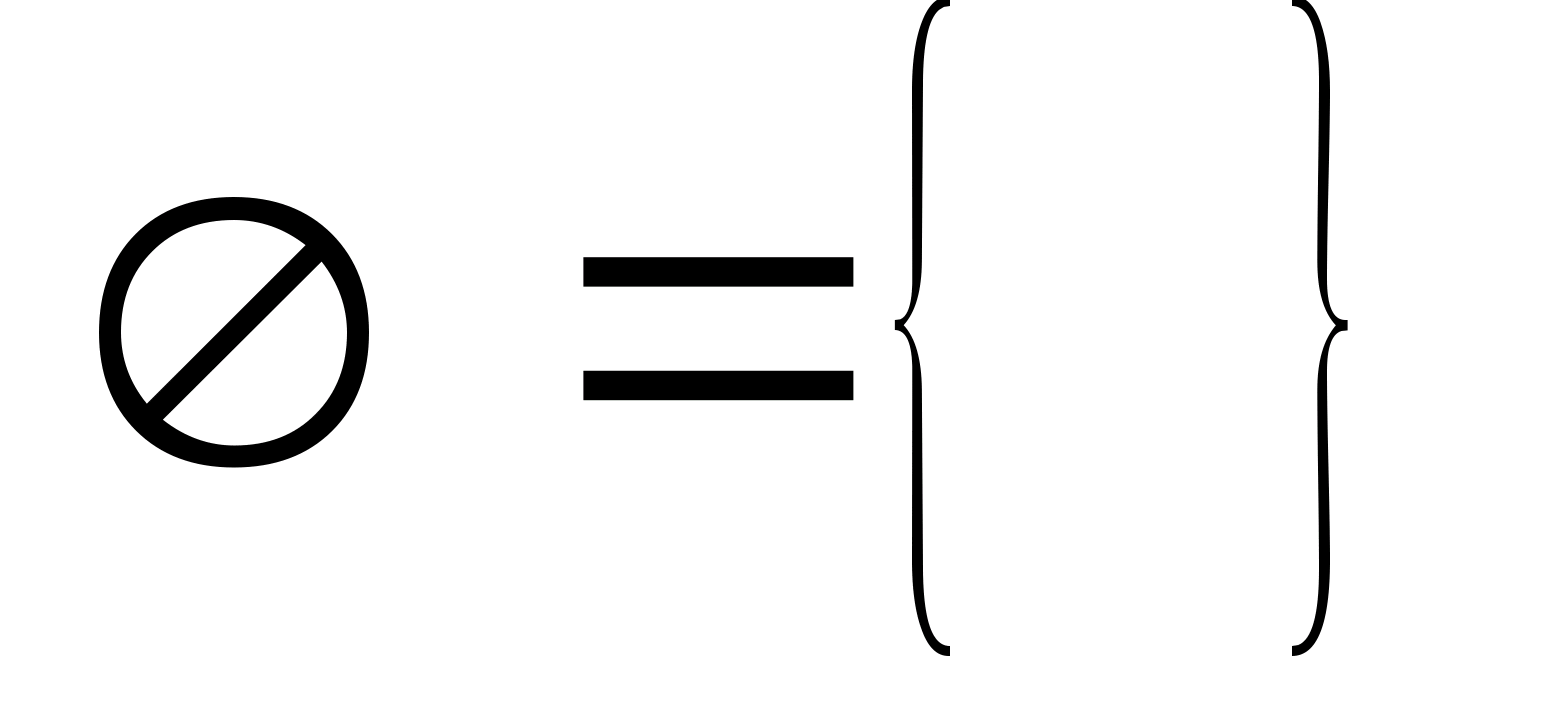, не содержащее ни одного элемента, называется пустым. Пустое множество является подмножеством любого другого. Множество, состоящее из пустого множества, само уже не является пустым.

Объединением (или суммой) множеств A и B называют множество

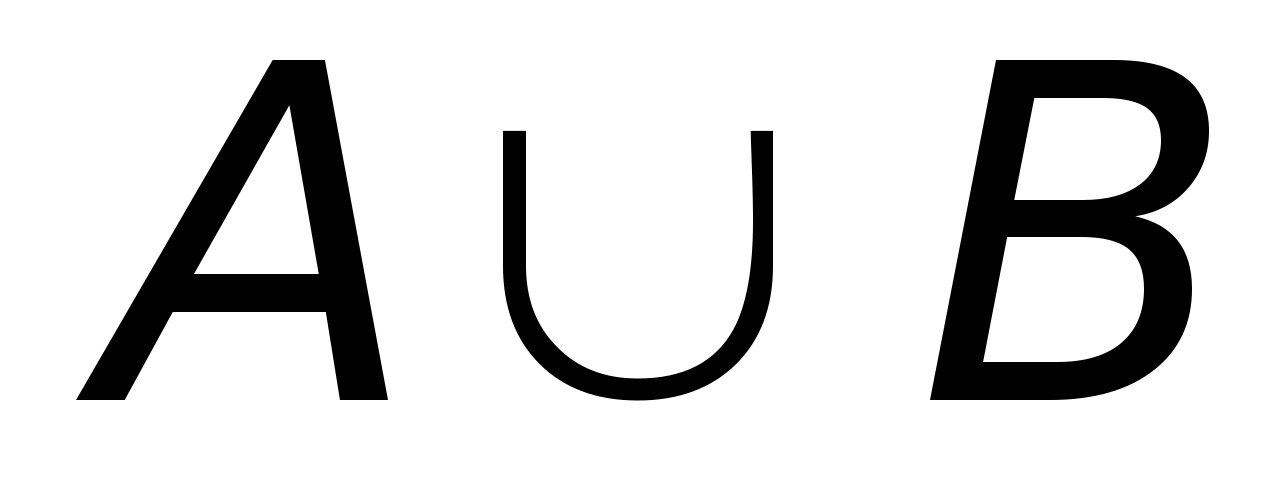, состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из множеств A или B (некоторый элемент принадлежит объединению множеств тогда и только тогда, когда он принадлежит или множеству A , или множеству B ).

Пересечением (или произведением) множеств A и B называют множество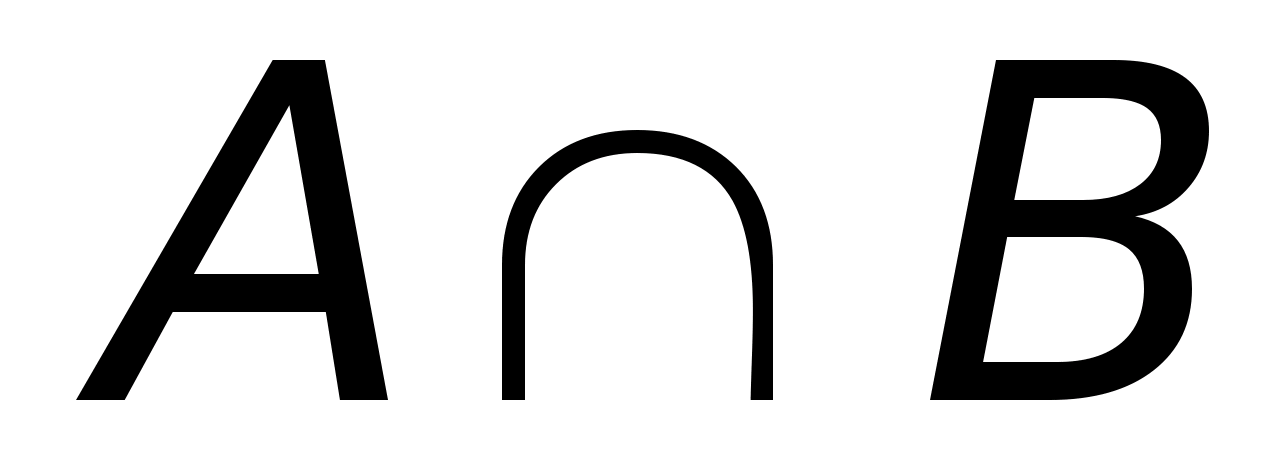

, состоящее тех и только тех элементов, которые принадлежат каждому из множеств A и B (некоторый элемент принадлежит пересечению множеств тогда и только тогда, когда он одновременно принадлежит и множеству A , и множеству B ).

Разностью множеств A и B называют множество

, состоящее из тех и только тех элементов, которые принадлежат множеству A , но не принадлежат множеству B (некоторый элемент принадлежит разности множеств тогда и только тогда, когда он одновременно принадлежит множеству A и не принадлежит множеству B ).

Если пересечение множеств A и B пустое:


,

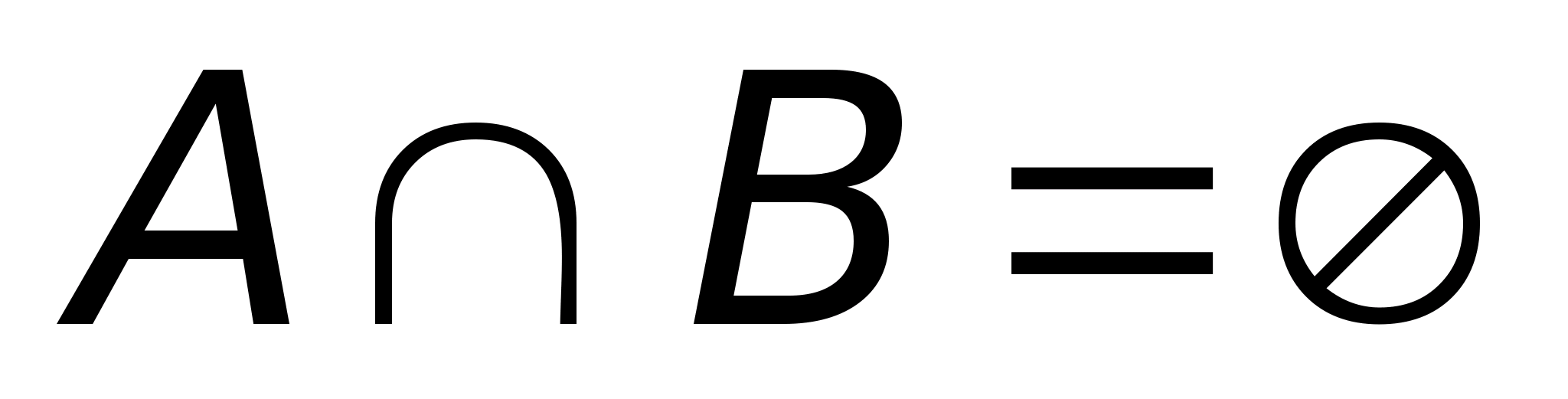то говорят, что множества A и B не пересекаются. В этом случае

,

.

Многие свойства операций объединения, пересечения и разности множеств аналогичны свойствам суммы, произведения и разности чисел, однако имеются и отличия.

1.

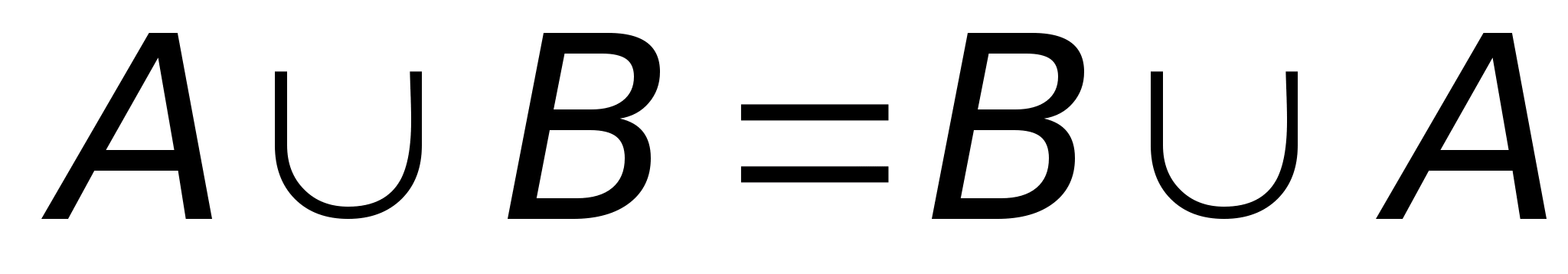(объединение коммутативно).

2. (пересечение коммутативно).

3. (объединение ассоциативно).

4. (пересечение ассоциативно).

5. (пересечение дистрибутивно относительно объединения).

6. (пересечение дистрибутивно относительно разности).

7.

.

9.

.

10.

.

11.

.

12.

.

3.2Целые, натуральные и рациональные числа

Натуральными числами называют числа, употребляемые для счета предметов и указания их порядкового номера. Множество натуральных чисел обозначают буквой N .

Любое натуральное число может быть записано в виде последовательности цифр . Если в записи числа важна как сама цифра, так и ее положение, то запись называют позиционной , а количество различных цифр называют основанием системы счисления . Так, при использовании арабских цифр и десятичной системы счисления запись «123» представляет число . Примером непозиционной записи является римская .

Множество натуральных чисел замкнуто по сложению и умножению : сумма и произведение двух любых натуральных чисел есть вновь натуральное число. Однако на множестве N вычитание выполнимо не всегда.

Рис. 4.1. Координатная ось

Проведем прямую (рис. 4.1), отметим на ней точку О – начало координат , выберем масштабный отрезок (длину его считаем равной единице) и направление. В этом случае говорят, что задана координатная ось . Каждому числу соответствует одна точка на координатной оси. Нулем называют число, соответствующее началу координат.

Начало координат разбивает координатную ось на два дополнительных луча; числа на одном луче называют положительными , числа на другом – отрицательными . Модулем числа называется расстояние от начала отсчета до соответствующей точки на координатной оси:

.

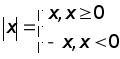Знаком числа называют число:

.

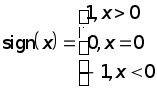Два числа x 1 и x 2 называют противоположными , если они имеют равные модули и различные знаки. Пишут: .

Множеством целых чисел Z называют объединение множества натуральных чисел, множества противоположных им чисел и множества, состоящего из нуля. Из определения следует .

На множестве Z всегда выполнимы три арифметические операции – сложение, вычитание и умножение. Однако множество Z не замкнуто по делению.

Множеством рациональных чисел Q называют множество, состоящее из чисел вида , где . Рациональные числа часто называют дробями , число m называется числителем дроби, число n – знаменателем дроби. Так как любое целое число может быть записано в виде дроби со знаменателем, равным единице, то .

Множество Q замкнуто по всем четырем арифметическим операциям.

3.3Иррациональные и действительные числа

Если точке не координатной оси не соответствует ни одно рациональное число, то говорят, что число x – иррациональное . Множество иррациональных чисел обозначают I .

Предложение . Числа n и n 2 либо оба нечетные, либо оба – четные.

Доказательство.

1. Пусть n нечетно: , где . Тогда:

где . Поэтому n 2 также нечетно.

2. Пусть n четно: , . Тогда:

,

где . Поэтому n 2 также четно.

Теорема 4.3.1 . Число – иррациональное.

Доказательство. Предположим, что существует несократимая дробь, квадрат которой равен двум:

Тогда , поэтому число – четное. Из доказанного выше следует, что m также должно быть четным: , . Поэтому:

Следовательно, число n также четное, и дробь будет сократимой. Полученное противоречие доказывает теорему.

Множеством R действительных чисел называют объединение множеств рациональных и иррациональных чисел:

Свойства множества R :

1. Множество R упорядочено : .

2. Множество R плотно : для любых , таких что , существует бесконечно много чисел , таких что .

3. Множество R непрерывно : если оно разбито на два непустых и непересекающихся подмножества A и B : , причем любое число из множества A меньше любого числа из множества B

существует единственное число c , такое что . При этом число c является либо наибольшим числом в множестве A (тогда в множестве B нет наименьшего числа), либо наименьшим числом в множестве B (тогда в множестве A нет наибольшего). Говорят, что число c является точной верхней гранью множества A :

(читается «супремум A »),

и точной нижней гранью множества B :

(читается «инфимум B »).

Из непрерывности множества R следует, что каждой точке на координатной оси соответствует действительное число, и наоборот, каждому действительному числу соответствует точка на координатной оси.

Отрезком (закрытым интервалом R , для которого

.

Полуоткрытыми интервалами называют подмножества, для которых

;

.

Интервалом (открытым интервалом ) называют подмножество множества R , для которого

Название Изображение Обыденный язык Формула (схема)
как пишется как читается
Конъюнкция (связки: и, а, но) & Λ х. p и q p Λ q Конъюнкция (p конъюнкция q)
Дизъюнкция (связки: или, либо) V + (нестрогая) V. +. p или q (нестрогая) p либо q (строгая) p V q Дизъюнкция p q (р дизъюнкция q)
Импликация (связка: если…, то) → Если p, то q p → q Импликация p q (р импликация q)
Эквиваленция (связка: тогда и только тогда, когда) ≡ p тогда и только тогда, когда q p ≡ q Эквиваленция p q (р эквиваленция q)
Отрицание (связка: не, нет) ¬ ~ − не р р Отрицание р (р с отрицанием)
Понятия A, B, C, D…
Субъект простого суждения S Схема простого суждения: S есть (не есть) P
Предикат простого суждения P
Простые суждения в составе сложных a, b, c, d….., p, q, r….
Кванторы общности кванторное слово «все» символ V
существования кванторное слово «некоторые» символ Ξ
Логический вывод «выводимо» символ ╞
Значение истинности «истинно» символ 1
Значение ложности «ложно» символ 0
Ограничения и порядок действий скобки (), , { }

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

Изучение дисциплины в течение одного семестра
Дневное отделение: лекции – 18, практические занятия – 18, самостоятельная работа студентов – 66. Аттестация: промежуточный контроль (проверка домашних заданий, тестирование), зачет.

ПРОГРАММА КУРСА
Тема 1. Предмет и значение науки логики. Формальный язык и семантические категории(лекция, практическое занятие) Процесс мышления и формы мысли. Значение логики. История л

Зачетные вопросы
1. Что является предметом формальной логики и в чем ее значение? 2. К чему приводит обобщение знания об отдельных предметах и их свойствах и отношениях? 3. Чем отличается логическ

Изучив "Логику", студенты должны
знать: ‑ историю возникновения и этапы развития логики, сущность, содержание и специфику логики как науки; ‑ сущность и содержание принципов логики, к

Методические рекомендации для студентов-заочников
Учитывая дистанционную форму обучения студентов заочного обучения, следует обратить внимание на следующие методические рекомендации. Первое.Студенты должны внимательно выс

Тема № 2. Законы логики и принципы правильного мышления
Введение. Общая характеристика основных законов логики. Закон тождества. Закон противоречия. Закон исключенного третьего. Закон достаточного основания. Заключение. Практическое зад

Тема № 3. Язык как знаковая система. Понятие знака
Введение. Понятие языковой формы. Языки естественные и искусственные. Функции естественного и искусственного языков. Знаковая система языка. Имя, предмет, функция. Заключение. Прак

Тема № 5. Основные характеристики знаков
Введение. Определение знака и знаковой системы. Типы знаков. Три вида знаковых отношений. Основные принципы семиотики. Заключение. Практическое задание: 1. Показани

Тема № 7. Общие принципы построения истинностных таблиц
Введение. Интерпретация пропозициональных переменных. Табличные определения пропозициональных связок. Логические отношения (по истинности и ложности) между формулами. Заключение. П

Тема № 8. Исчисление высказываний
Введение. Пропозициональная логика. Общезначимость исчисления высказываний. Пропозициональные связки. Язык логики высказываний. Заключение. 1.Записать символически выск

Тема № 10. Понятие как форма мышления. Общая характеристика
Введение. Определение понятия. Классификация признаков. Содержание и объем понятия. Понятие и термин. Заключение. Практическое задание: 1.Каки

Тема № 11. Логическая структура и основные характеристики понятия
Введение. Виды понятий. Отношения между понятиями. Заключение. Практическое задание: 1.Дайте полную логическую характеристику понятиям (единич

Тема № 14. Значение понятий в познании
Введение. Понятие как член логической связи. Логические ошибки в понятиях. Заключение. Практическое задание: 1.Приведите пример логической свя

Тема № 16. Виды понятий Обобщение и ограничение понятий
Введение. Виды понятий по содержанию. Виды понятий по объему. Обобщение понятий. Ограничение понятий. Заключение. Практическое задание: 1.Дайт

Тема № 17. Виды отношений между понятиями по содержанию и объему
Введение. Отношения между понятиями по содержанию. Отношения между понятиями по объему. Графическая иллюстрация отношения понятий по объему. Заключение. Практическое задание:

Тема № 21. Категорические суждения
Введение. Деление суждений по количеству. Деление суждений по качеству. Объединенная классификация категорических суждений в «логическом квадрате». Распределенность терминов в суждении. Заключение.

Тема № 22. Логические отношения между категорическими суждениями
Введение. Отношения несовместимости. Отношения совместимости. Графическая схема отношений (логический квадрат). Зависимость истинности или ложности суждений от их отношений. Заключение.

Тема № 23. Сложные суждения
Введение. Характеристика конъюнктивных, дизъюнктивных, импликативных и эквивалентных суждений. Сводная таблица истинности (ложности) этих суждений Заключение. Практическое задание:

Тема № 26. Общие правила простого категорического силлогизма
Введение. Правила терминов. Правила посылок. Правила фигур. Понятие о модусах фигур силлогизма. Заключение. Практическое задание: 1. Какое

Тема № 28. Индуктивные умозаключения
Введение. Понятие об индукции. Полная индукция. Неполная индукция. Индукция через простое перечисление. Научная индукция. Заключение. Практическое задание:

Тема № 29. Методы установления причинной зависимости явлений
Введение. Причинная связь явлений. Пять методов установления причинной связи. Умозаключения по аналогии. Заключение. Практическое задание: 1.О

Тема № 30. Гипотеза
Введение. Общая характеристика гипотезы. Виды гипотез. Развитие гипотезы. Проверка гипотезы. Фактическое (решающий опыт) и логическое доказательства гипотезы. Практическое задание:

Тема № 35. Ошибки в доказательствах
Введение. Подмена доказываемого тезиса. Ошибки в основаниях доказательств. Ошибки в способе доказательства. Ошибки омонимии и амфиболии. Ошибка ложного следования. Заключение. Прак

Логика и язык
Язык – это знаковая система, материальная форма, посредством которой люди выражают мысли. Язык имеет пять видов: линий, звуков, жестов, цвета и запаха, и три формы: естественный, ко

Связь между мышлением и языком
Язык и мышление неразрывно связаны между собой. С помощью языка мы излагаем мысли в определенной, общедоступной форме. Этому способствуют понятийные стереотипы, которые накладывают ограничения на и

Логическое и психологическое
Рассуждая логически, мы следуем тем принципам и правилам, которые указывают, как следует делать «правильные» выводы. Принципы логики устанавливают нормы, по которым мы оцениваем качество чьих-либо

Семантические категории
Логическая семантика изучает отношения знака и значения, правила перевода абстрактных символов на язык содержательного знания. В логике важно найти совместимость естественного и искусственного язык

Процесс мышления и формы мысли
Существует много способов представить процесс мышления. Для биолога ‑ это активация групп нейронов, для психолога – это комбинация в сознании ряда образов, для кибернетика – это процесс перед

Общая характеристика понятия
Логическое мышление представляет собой различные связи мыслей. Если вглядеться в суждение, то мы увидим, что оно состоит из некоторых мыслей, которые многократно встречались нам в других суждениях

Понятие и представление
Всякое понятие есть мысль о признаках предмета. Однако не всякая мысль о признаках есть понятие. В чувственном познании представление тоже есть мысль о признаках предмета. Представить предмет – это

Признаки понятия
Те мысли, которые образуют целостность суждения, называются понятиями. Мысль о предмете есть понятие только при условии, если мыслимый предмет имеет сходство или различие с другими предметами, то е

Виды понятий
Всякое понятие имеет две логические характеристики – содержание и объем. Существенные признаки предмета составляют содержание понятия. Бессодержательных понятий не

Функции понятий
Язык является средством мышления. Он выражает понятия, которые выполняют множество функций. Из них основными являются следующие: 1. Символическая функция. Понятие становится символо

Вопросы для самопроверки
1. Перечислите признаки предмета в логической классификации. 2. Чем различаются: слово, понятие, термин? 3. Что такое содержание и объем понятия? 4. Объясните смысл закон

Определение понятий
Определение понятий (definitio) – одна из важнейших логических операций, которую мы постоянно совершаем как в повседневной жизни, так и в научном процессе. Смысл ее заключается в том, что, раскрыва

Неявные определения
Если нельзя определить понятия через родовые и видовые признаки, то используют описание отношений между определяемыми понятиями. Особенность таких определений состоит в том, что предмет определяетс

Ограничение и обобщение понятий
В процессе мышления часто приходится конкретизировать знания о предмете мысли. Уточняя понятие, мы вводим новые признаки, тем самым увеличивая его содержание, но при этом объем понятия уменьшается.

Деление понятий
Предметы, которые мыслятся в понятии, составляют известное множество, которое включает в себя отдельные группы предметов. В процессе деления мы выясняем, из каких подмножеств состоит исходное множе

Вопросы для самопроверки
1. Что такое деление понятия? 2. Чем отличается дихотомическое деление от видообразующего? 3. Каким принципам подчиняется классификация? 4. Какие функции выполняет класси

Общая характеристика суждения
Суждение – это развернутое понятие; поскольку понятие заключает в себе некоторые признаки предмета мысли, то суждение – это такая форма мысли, в которой выражена связь между предметом мысли и его п

Структура суждения
Суждение как логическая форма состоит из следующих элементов: субъекта, предиката и связки. Субъект (лат. subjectum – лежащий в основе, подлежащее) ес

Модальность суждений
Модальность суждения (лат. мodus – способ, мера, наклонение) выражает степень существования, свойства, отношения, отображенного в суждении. При этом в суждении утверждается или отрицается действите

Зависимость познавательного значения суждения от его формы
Значение или важность суждения для знания зависит во многом от его формы. Так, условные и разделительные суждения становятся ценными для знания лишь в связи с категорическими суждениями. В

Определите модальность суждения. Приведите их схемы.
Пример: А). Ухта южнее Воркуты. – Суждение об отношении места. xRy = R(x,y). Б). Нет дыма без огня. – Суждение существования. Р есть. В).

Составьте схемы сложных суждений.
Пример: Эмиссия есть изготовление и выпуск в обращение денег или ценных бумаг Схема: S есть Р(Р¹ Λ Р² V Р³) &nb

Выделите три группы суждений: а) совместимые, б) несовместимые, в) частично совместимые.
Пример: Ни один волос не упал с его головы. Многие хотели его видеть. Он лишился всех своих волос. Некоторые гайки имеют правую резьбу. Все пришли вовремя.

Табличное определение истинности (ложности) сложных суждений.
Выше мы уже говорили о том, что суждение может быть классифицировано либо как истинное, либо как ложное, но не то и другое вместе. «Истинность» или «ложность» повествовательного предложения, которы

Вопросы для самопроверки
1. Что такое преобразование суждения? 2. Чем отличается обращение суждения от превращения суждения? 3. Каким принципам подчиняется истинность (ложность) суждения? 4. Каку

Общая характеристика умозаключения
Если основной задачей логики является составление приемов приобретения и доказательства знаний, то одним из главных приемов является умозаключение. Умозаключением называется такой прием мышления

Непосредственные умозаключения
Мы можем получать вывод из посылок путем преобразования последних. Истинность вывода в этом случае целиком зависит от истинности посылок, если, разумеется, не нарушены правила преобразования, котор

Силлогизм
Силлогизм (греч. syllogismos – сосчитывание) – это вид умозаключения, в котором требуется определить, следует ли из двух или нескольких суждений данный вывод. Признав истинность пос

Энтимемы
В практике нашего мышления, как обыденного, так и научного, мы пропускаем либо одну из посылок, либо заключение. Такие силлогизмы, в которых та или иная часть не выражена в явной форме, называются

Условные силлогизмы
Если в силлогизме обе посылки взяты как условные суждения, то заключение также будет условным суждением, а силлогизм будет опосредованным условным умозаключением. Если А

Упражнения
А) Определите модальность суждения. Приведите их схемы. Пример: 1). Ухта южнее Воркуты. – Суждение об отношении места. xRy = R(x,y). 2). Нет дым

Упражнения
А). Укажите, какие из приведенных умозаключений получены с помощью полной, а какие с помощью неполной индукции: 1). Все студенты нашей группы прошли практику. 2). Угол падения равен углу отражения.

Метод сходства
Этот метод представляет собой умозаключение, основанное на сравнении нескольких случаев наступления одного и того же явления и выявления действительной причины на основе единственного сходства. Нап

Метод различия
Для умозаключения по этому методу необходимо иметь два случая: случай, в котором исследуемое явление наступает, и случай, в котором оно не наступает. При этом они подбираются так, чтобы были сходны

Соединенный метод сходства и различия
В этом методе соединились оба предшествующие правила, поэтому его можно сформулировать так: если два или более случаев наступления наблюдаемого явления сходны только в одном предшествующем обсто

Метод сопутствующих изменений
В основе метода сопутствующих изменений лежит принцип причинно-следственной связи, который гласит, что всякое изменение причины вызывает соответственное изменение следствия; и наоборот, всякое изме

Метод остатков
В основе этого метода лежит следующее наблюдение: если сложное явление есть результат сложной причины, то каждый простой элемент этого явления вызывается простым элементом сложной причины, соответс

Вопросы для самопроверки
Что необходимо для нахождения действительной причины или действительного следствия? На чем основан «метод сходства»? Что необходимо умозаключению по «методу различ

Упражнения
Определите, какие методы установления причинной связи применимы, запишите их в виде схемы и в виде суждений, образующих причинно-следственную связь. Картофель, проросший в темном пог

Аналогичные умозаключения
Умозаключения по аналогии (греч. analogia – подобие, сходство) относится к модификации традуктивного типа умозаключений. Отличие заключается лишь в том, что в основе традукции лежит тождество, уста

Упражнения
Определите вид аналогии, запишите их в виде схемы и в виде суждений, образующих связь предметов или отношений. Пример: При исследовании горных пород в Ав

Понятие доказательства
Связь между понятиями и суждениями, которыми мы пользуемся для выражения мыслей, ‑ это отражение связи предметов, их признаков, их отношений и их законов. Но истинность суждений не о

Упражнения
Выделите тезис и аргументы. Выберите одну из форм умозаключения и постройте демонстрацию. Пример: Студент Петров сдал дипломный проект досрочно, так как оче

Правила доказательства и опровержения
В процессе доказательства возможны ошибки, возникающие при умышленном или не умышленном нарушении правил. Правила доказательства делятся на три группы в соответствии со структурой доказательства: п

Виды доказательств
По цели доказательства делятся на: 1) доказательство истинности тезиса и 2) доказательство ложности тезиса. Первое, имеющее целью установление истинности тезиса, называется про

Вопросы для самопроверки
1.Какие три группы правил в доказательстве вы знаете? 2.Чем объясняется ясность и четкость в формулировании тезиса? 3.Что такое «подмена тезиса»? 4.Почему истинность аргу

Упражнения
Подберите аргументы и постройте прямое доказательство тезиса. Пример: Студента Иванова вызвали в суд для дачи свидетельских показаний. Аргументами

Понятие гипотезы и условия её появления
Слово гипотеза (греч. hypothesis – предположение) имеет несколько значений. Во-первых, это догадка о факте, который пока недоступен для обнаружения, но может проявиться с вероятностью, близкой к

Построение гипотезы
Построение гипотезы - это сложный логический процесс с участием различных форм умозаключений. В одних случаях гипотеза возникает как результат сравнения двух единичных явлений, т.е. ее основой выст

Развитие гипотезы
Гипотеза не сводится к выдвижению предположения, а проходит процесс развития, в ходе которого она корректируется, дополняется новыми предположениями и либо опровергается и заменяетс

Подтверждение гипотезы
Чтобы превратиться в достоверное знание, предположение подлежит научной и практической проверке. Процесс проверки гипотезы, протекающий с использованием различных логических приемов

Упражнения
Подберите факты и постройте гипотезу. Пример: В известном кинофильме «Земля Санникова» было высказано предположение, что в Северном Ледовито

Закон тождества
Следует отметить, что всякая правильная мысль должна быть определенной. Это значит, что в процессе рассуждения нельзя подменять один предмет мысли другим. Например, в рассуждении «жизнь бьет ключом

Закон противоречия
Из закона тождества следует, что никакая мысль не может быть тождественна мысли её отрицающей, то есть, чтобы быть понятым, необходимо соблюдать требование непротиворечивости мысли

Закон исключенного третьего
То, что мысль может быть приравнена либо к истине, либо ко лжи, следует из закона исключенного третьего: из двух взаимоотрицающих суждений одно непременно истинное в данное время, в данном месте

Закон достаточного основания
Правильность или истинность мысли обусловлена достаточным для них основанием. Действительно, мы можем считать ту или иную мысль истинной лишь после того, как приведены основания, являющиеся уже про

Вопросы для самопроверки
1. Что называется законами мышления? 2. Почему законы мышления называют формальными законами? 3. Как формулируется закон тождества? 4. Как формулируется закон противоречи

Упражнения
Определите, требование какого логического закона нарушено в следующих рассуждениях. Пример: Этот студент не раскрыл основное содержание темы, но заслужив

ОСНОВНЫЕ ЛОГИЧЕСКИЕ ПОНЯТИЯ
АКСИОМА (гр. axioma -значимое, достойное уважения, бесспорное) - истинное суждение, которое при дедуктивном построении какой - либо теории принимается без доказательств в качестве и

Правила фигур
№ Фигура Правильные модусы

Правила терминов
№ Правило Пример ошибки Примечания В силлогизме должны быть только три термина Движение –

Правила посылок
№ Правило Пример ошибки Примечсния Из двух отрицательных посылок нельзя сделать никакого

По отношению к тезису
Правила Ошибки 1. Тезис должен быть ясным и четким 1. Выдвижение неясного, неточного тезиса 2. Тезис должен

ГЛОССАРИЙ
ЗАКОН ЛОГИКИ – устойчивая, существенная, повторяющаяся связь мыслей; обладает следующими свойствами: а) определенность (представление предмета в одних и тех же признаках); б) посл

Математика характерно широкое использование символики, которая, до сути, является аппаратом формальной логики. Формальная, или символическая, логика - это специальный метод познания структуры мышления. Такой разработанный аппарат используют везде. В математике многие важные положения удается записывать в виде символов. Запись логических рассуждений в символах придает доказательствам более краткий, простой вид. Формальная логика оперирует высказываниями (из них, кстати, состоит и наша речь). Высказыванием называют предложение, относительно которого имеет смысл утверждать, что оно истинно или ложно. Пример 1.3. „Москва - столица России**, „Петров И.И. - студент МГТУ ", х2+у2 = 1, х € R - высказывания; х2 -2х + + У2 - не является высказыванием. # Соединяя простые высказывания словами „и", „или", „не", „если..., то", мы получаем более сложные высказывания, которые определяют нашу речь. В математике эти слова называют логическими связками, в формальной логике они соответствуют основным логическим символам, на которых мы кратко и остановимся. 1. Конъюнкцией pAq высказываний р и q называют высказывание, которое истинно тогда и только тогда, когда оба высказывания (и р, и q) истинны. Логический симвЪл конъюнкции А заменяет в речи союз „и". Конъюнкцию обозначают также р & q. 2. Дизъюнкцией pW q высказываний р и q называют высказывание, которое ложно в том и только в том случае, когда оба высказывания ложны, а истинно, когда хотя бы одно из них (р или q) истинно. Логический символ дизъюнкции V в речи заменяет слово „или". 3. Импликацией р => q высказываний р и q называют высказывание, которое ложно тогда и только тогда, когда р истинно, a q - ложно. Логический символ импликации => используют при указании на последствия некоторого факта. Он заменяет слова „если..., то". Можно также читать „р влечет qu. 4. Логический символ эквиваленции & означает, что высказывание р q истинно тогда и только тогда, когда оба высказывания р и q истинны или оба высказывания ложны. Этот символ заменяет в речи слово „равносильно". 5. Отрицанием высказывания р называют высказывание -»р, которое истинно, если р ложно, и ложно, когда р истинно. Логический символ -» в речи заменяет слово „не". Для сокращения и уточнения записи высказываний вводят два знака V и 3, называемых соотвеНекоторые основные логические символы. Формальная, или символическая, логика. тственно кванторами общности и существования. Выражение „для всякого элемента х множества Еи записывают в виде Vs 6 Е. Эта запись означает, что утверждение, следующее за ней, будет выполнено для произвольного элемента множества Е. Запись V&i, «2» хп€Е означает: „каковы бы ни были элементы xi, 32, хп множества Еи. Выражение „существует по крайней мере один элемент множества Е, такой, что..." заг писывают Зх £ Е: ... Все, что следует за этой записью, выпол- дается хотя бы для одного элемента множества Е. Наоборот, $х е Е: ... означает, что все следующее далее не выполняется ни для одного элемента из Е. Выражение „ существует один и только один элемент из Е, такой, что...u записывают в виде Э!ж € Е: ... Запись Зх\} хз, хп € Е: ... означает: ясуществуют такие элементы х\у а?2» » я» множества Е, что...ц. Введенными символами удобно пользоваться, например, при определении операций над множествами. Так, AUB:<*{х: (х € А) V (х € В)}, АПВ:*>{х: {х € А) Л (ж € В)}, А\В:*>{х: {х € А) Л (х g В)}, А:<${х: (ж €Й)Л(х£ Л)}, где символ означает эквивалентность по определению. Связь теории множеств и формальной логики достаточно широка. Исследованием этой связи впервые занимался английский математик Джордж Буль (1815-1864), работы которого положили начало одному из важнейших направлений современной алгебры, называемому булевой алгеброй. Ясно, что взятие дополнения тесно связано с отрицанием высказывания, операции объединены и пересечения множеств - с дизъюнкцией и конъюнкцией высказываний соответственно, включение подмножества в множество - с импликацией, а равенство множеств - с эквиваленцией высказываний. В силу этой связи с помощью теории множеств можно решать некоторые логические задачи. Пример 1.4. Рассмотрим набор высказываний: 1) животные, которых не видно в темноте, серы; 2) соседи не любят тех, кто не дает им спать; 3) кто кредко спит, громко храпит; 4) соседи любят животных, которых видно в темноте; 5) все слоны крепко спят; 6) кто громко храпит, не дает спать соседям. Эти высказывания можно перевести на язык теории множеств, если ввести следующие обозначения: А - множество тех, кто будит соседей; В - множество тех, кто крепко спит; С - множество тех, кто громко храпит; D - множество животных, которых видно в темноте; Е - множество слонов; F - множество тех, кого любят соседи; G - множество тех, кто серые. Высказывание 1) означает, что элементы, не лежащие в D) содержатся в G, т.е. 1) D С G. Остальные высказывания принимают вид: 2) Л С F; 3) £ С С; 4) D С F; 5) Е С В; б)ССЛ. Взяв дополнения множеств D и F, из 4) согласно принципу двойственности получим F С D и затем соединим все выскаг зывания в цепочку ECCCACFCDCG. Из этой цепочки (с учетом свойства транзитивности символа включения) следует, что ECGy т.е. все слоны серы. # Рассмотренные логические символы и кванторы существования и общности широко используют математики для записи предложений, в которых они, по сути, воплощают плоды своего творчества. Эти предложения представляют собой устанавливающие свойства математических объектов теоремы, леммы, утверждения и следствия из них, а также различные формулы. Однако следует отметить, что часть предложений приходится все же выражать словами. Любая теорема состоит, вообще говоря, в задании некоторого свойства Л, называемого условием, из которого выводят свойство Ву называемое заключением. Коротко теорему пА влечет Ви записывают в виде А В и говорят, что А является достаточным условием для Б, а Б - необходимым условием для А. Тогда обратная теорема имеет вид В А (возможна запись при помощи обратной импликации А <= В), но справедливость прямой теоремы еще не гарантирует справедливости обратной ей теоремы. Если справедливы данная тедрема и обратная ей, то свойства А я В эквивалентны, и такую теорему можно записать в виде А о В. Эта запись соответствует фразам: „Для того, чтобы Л, необходимо и достаточно, чтобы В", „А тогда и только тогда, когда Ви или „А, если и только если Ви. Ясно, что в этих фразах А и В можно поменять местами. Утверждение, противоположное утверждению А} записывают -^Л, что соответствует словам „не Аи. Если в символьную запись утверждения А входят кванторы 3, V и условие Р, то при построении символьной записи противоположного утверждения -*А квантор 3 заменяют на V, квантор V - на 3, а условие Р заменяют на условие -»Р. Пример 1.6. Рассмотрим утверждение Зх € Е: Р (существует элемент х множества Е, обладающий свойством Р) и построим его отрицание. Если это утверждение неверно, то указанного элемента не существует, т.е. для каждого х € Е свойство Р не выполняется, или -.(За: 6 Е: Р) = Vx € Е: -.Р. Теперь построим отрицание утверждения Vx 6 Е: Р (для каждого элемента х множества Е имеет место свойство Р). Если данное утверждение неверно, то свойство Р имеет место не для каждого элемента указанного множества, т.е. существует хотя бы один элемент х € Е, не обладающий этим свойством, или -.(УхбЕ: Р) = Зх€Я: -чР. # Доказательство предложения представляет собой проводимое по определенным правилам рассуждение, в котором для обоснования сформулированного предложения используют определения, аксиомы и ранее доказанные предложения. Примеры доказательств свойств абсолютных значений действительных чисел приведены доше (см. 1.3), а первого из соотношений свойства дистрибутивности операций объединения и пересечения и первого из законов де Моргана (1.7) - в 1.4. Одним из используемых приемов является метод доказательства от противного. Для доказательства таким методом теоремы А => В предполагают, что верно -«В. Если рассуждения приводят к тому, что при таком предположении условие А невыполнимо, т.е. возникает противоречие, то теорему считают доказанной. Пример 1.6. Используем метод доказательства от противного, чтобы убедиться в справедливости второго закона де Моргана (1.7) AC\B = AUB. Если это равенство верно, то каждый элемент х € А П В должен принадлежать и A U В, т.е. х € A U В. Предположим противное: s £ AUB. Тогда по принципу двойственности (см. 1.4) х € АПВ, т.е. х ^ АПВ, а это противоречит исходному условию х € А П В, что доказывает справедливость импликации высказываний х€ АГ\В=>хе лив. Наоборот, каждый элемент х 6 A U В должен принадлежать и Л Г) В, т.е. х € А О В. Снова предположим противное: х £ i АП В, т.е. х £ АП В, или (хбА)Л(хбВ). Тогда (х£А)Л Л (х £ В) и х £ AUB, а это опять противоречит принятому условию х £ A U В, что доказывает справедливость обратной импликации высказываний х€ АПВ«=х€ AUB. Некоторые основные логические символы. Формальная, или символическая, логика. В итоге справедливость второй формулы (1.7) доказана полностью. # При доказательстве предложений, справедливых для произвольного натурального числа п G N, иногда применяют метод математической индукции: непосредственной проверкой устанавливают справедливость предложения для нескольких первых значений п (n= 1, 2, ...), а затем предполагают, что оно верно для п = к} и если из этого предположения следует справедливость данного предложения для п = к -f 1, то его считают доказанным для всех п € N. Пример 1.7. Докажем справедливость формулы «П = «1 (1.8) для суммы первых п членов геометрической прогрессии 0|, a2 = aitf, a3 = alq2) an = aign_1 со знаменателем прогрессии q ^ 1. Ясно, что формула верна для п= 1 и п = 2. Предположим, что она верна и для п = к, т.е. Некоторые основные логические символы. Формальная, или символическая, логика. Если в (1.9) обозначить к +1 = п, то снова придем к (1.8), что доказывает справедливость этой формулы.

Кванторы

 - общности

 - существования

Связки

 - конъюнкция (и)

v - дизъюнкция нестрогая (или)

 - дизъюнкция строгая (или)

 - импликация (если..., то...)

 - эквиваленция (если и только если..., то...)

] - отрицание (неверно, что...)

Символы для модальных операторов

М - модальность

V - доказано (верифицировано)

F - опровергнуто (фальсифицировано)

О - обязательно

F - запрещено

Р - разрешено

 - необходимо

] - случайно

 - возможно

] - невозможно

Глава I. Предмет и значение логики

§ 1. Роль мышления в познании...............……………………. 5

§ 2. Понятие о форме и законе мышления.................……….. 8

§ 3. Основные логические законы................……………….. 12

§ 4. Язык логики....................... ……………………………. 18

§ 5. История логики (краткий очерк) ...................…………. 23

§ 6. Значение логики..................... …………………………... 27

Контрольные вопросы................... ………………………….. 29

Глава II. Понятие

§ 1. Понятие как форма мышления....................…………… 30

§ 3. Виды понятий..............................……………………... 36

§ 4. Отношения между понятиями.....................……………. 40

Контрольные вопросы............................…………………… 44

Глава III. Логические операции с понятиями

§ 1. Обобщение и ограничение понятий.................……… 45

§ 2. Определение понятий..........................…………………. 47

§ 3. Деление понятий.............................…………………..... 54

§ 4. Операции с классами..........................…………………. 60

Контрольные вопросы............................……………………. 62

Глава IV. Суждение

§ 1. Суждение как форма мышления...................……….... 63

§ 2 Простые суждения................. …………………………… 66

§ 3. Сложные суждения...........................………………….. 78

§ 4, Логические отношения между суждениями.............…. 86

§ 5. Модальность суждений...............………………………. 94

Контрольные вопросы.............. …………………………...105

Глава V. Логика вопросов и ответов

§ 1. Виды вопросов............................……………………..... 108

§ 2. Виды ответов................. ………………………………...112

Контрольные вопросы. . ……………… .......................... 116

Глава VI. Дедуктивные умозаключения. Выводы из простых

суждений

§ 1. Умозаключение как форма мышления. Виды умозаключений …………………………………………………. 119

§2. Непосредственные умозаключения.... …………………121

§ 4. Умозаключения из суждений с отношениями ……….. 141

Контрольные вопросы............................…………………… 143

Глава VII. Дедуктивные умозаключения. Выводы из сложных суждений. Со­кращенные и сложные силлогизмы

§ 1. Чисто условное и условно-категорическое умозаключения.... ………………………………………………..144

§ 3. Условно-разделительное умозаключение …………. ... 151

§ 4. Сокращенный силлогизм (энтимема). ................……... 153

§ 5. Сложные и сложносокращенные силлогизмы.........… 155

§ 6. Понятие о логике высказываний …………………………….157

Контрольные вопросы ……………………………………………160

Глава VIII . Индуктивные умозаключения

§ 1. Полная индукция……………………………………..…162

§ 2. Неполная индукция. Популярная индукция ………….165

§ 3. Научная индукция ……………………………………...168

§ 4. Статистические обобщения.......……………………...181

Контрольные вопросы.............………………………….….183

Глава IX. Умозаключения по аналогии

§ 1 Понятие аналогии...............…………………………….184

§ 2. Виды аналогии.................………………………….…..185

§ 3. Условия состоятельности выводов по аналогии …....187

§ 4. Роль аналогии в науке и правовом процессе………....189

Контрольные вопросы..........………………………………194

Глава X. Логические основы аргументации

§ 1 Аргументация и доказательство.…………………………….195

§ 2. Состав аргументации: субъекты, структура……………….197

§ 3. Способы аргументации: обоснование и критика ……………202

§ 4. Правила и ошибки в аргументации………………………….212

§ 5. Поля аргументации………………………………………....224

Контрольные вопросы………………………………………....230

Глава XI. Гипотеза

§ 1. Понятие и виды гипотез. Версия………………………….…231

§ 2. Построение гипотезы (версии)………………..……………..236

§ 3. Проверка гипотезы ………………………………………….241

§ 4. Способы доказательства гипотез …………………………...244

Контрольные вопросы…………………………………….…..247

Литература……………………………………………..………...248

Предметный указатель………………………………………….249

Логические символы…………………………………………...252

1От греческого словаlogos- «мысль», «слово», «разум», «закономерность».Термин «логика» употребляется также для обозначения закономерностей объектив­ного мира (например, «логика фактов», «логика вещей», «логика политической борь­бы» и т.п.); для обозначения строгости, последовательности, закономерности процес­са мышления («логика мышления», «логика рассуждений»). Закономерный характер мышления является своеобразным отражением объективных закономерностей. Логи­ка мышления есть отражение логики вещей.

2От латинского словаratio- «разум», рациональное познание - познание спомощью разума, мышления.

4От латинского термина abstractio - отвлечение. Абстрагирование - процесс отвлечения от некоторых свойств предметов, позволяющий выделить другие его свой­ства. Абстракция - результат абстрагирования.

1Согласно традиции этот закон принято называть законом противоречия. Од­нако название - закон непротиворечия - точнее выражает его действительный смысл.

2О несовместимых суждениях см. гл. IV, § 4.

2Учитывая европейские традиции, в русле которых в основном развивалась ло­гика в России, мы не останавливаемся здесь на формировании и развитии логических учений в странах Востока, где сложились оригинальные концепции таких мыслите­лей, как Ибн Сина (Авиценна), Ибн Рушд (Аверроэс) и др.

3Математической логикой называют также особый раздел современной матема­тики, исследующий специфику математических рассуждений и доказательств.

1 В «Энциклопедии философских наук» Гегель сформулировал эту мысль следу­ющим образом: «Мыслить, как полагают, может всякий и без помощи логики, подоб­но тому как мы можем переваривать пищу, не изучая физиологии» (Энциклопедия философских наук. М., 1975. Т. 1. С. 110). Создавая диалектическую логику, Гегель критиковал логику формальную, однако он не отрицал ее значения. Высоко оценивая Аристотеля как основателя формальной логики, Гегель в той же работе писал: «Изу­чение этой формальной логики, без сомнения, приносит известную пользу; это изуче­ние, как принято говорить, изощряет ум. Мы приучаем концентрировать мысль, при­учаемся абстрагировать, между тем как в обычном сознании мы имеем дело с умствен­ными представлениями, перекрещивающимися и перепутывающимися друг с дру­гом». (Там же. С. 115-116.)

2Бирюков Д.Л. Физиологическое учение И.П. Павлова - острое оружие в борь­бе против религии. Л., 1953. С. 20.

3Клини С.К. Математическая логика. Л., 1973. С. 79.

1Судебные речи известных русских юристов. М., 1958 С. 22.

1Сущность как совокупность всех внутренних, необходимых свойств и связей предмета, взятых в их естественной взаимозависимости, отражается в научных поня­тиях, которые формируются на основе всестороннего исследования предмета и про­никновения в его внутреннюю природу с помощью научных методов познания. Тер­мин «существенный признак» нередко употребляется для обозначения признаков предмета, которые хотя и не раскрывают его действительной сущности, но являются важными для его характеристики.

1Слова и словосочетания, имеющие определенный смысл и обозначающие какой-либо предмет, называются именами. См об этом гл. I, § 4.

1Не следует смешивать логическую характеристику понятий как положитель­ных и отрицательных с политической, нравственной, юридической оценкой тех явле­ний, которые они отражают Так, понятия «агрессия», «преступность», «алкоголизм» являются положительными их содержание составляют признаки, принадлежащие предмету Однако явления, отраженные в этих понятиях, вызывают у нас отрицатель­ную оценку.

1Обычно указывают ближайший род, который содержит больше признаков, общих с признаками определяемого понятия (подведение понятия «чек» под понятие «документ» осложнит задачу определения) Поэтому в логической литературе дан­ный вид определения называется иногда определением через ближайший род и видо­вое отличие.

1Один из героев пьесы Мольера «Мнимый больной» построил свое рассужде­ние о причине усыпляющей силы опиума следующим образом: опиум усыпляет пото­му, что он имеет усыпляющую силу, а усыпляющую силу опиум имеет потому, что он усыпляет.

2От греческого - «то же самое слово».

1Кони А.Ф. Избранное. М., 1989. С. 54.

1От собственно вопросительных предложений следует отличать предложения вопросительно-риторические (риторический вопрос), содержащие утверждение или отрицание в форме вопроса. Например. «Кто же этого не знает 9 », «Разве можно так поступать?». Эти предложения выражают суждения «Это знают все», «Так поступать нельзя». Они могут быть как истинными, так и ложными.

1Так как для русского языка характерен подвижный порядок слов, члены пред­ложения и термины суждения могут занимать различные позиции. Например: «Беле­ет парус одинокий / В тумане моря голубом» (Лермонтов). Субъектом этого суждения является понятие «одинокий парус», предикатом - понятие «белеет в голубом тума­не моря». Связка грамматически не выражена. Поэтому при логическом анализе по­добных суждений прежде всего из художественных произведений, особенно поэти­ческих, важно правильно определить субъект, предикат и связку.

1Слова «все», «ни один», «некоторые» и другие, характеризующие суждение со стороны его количества, называются кванторными словами (от латинского quan­tum - «сколько») Введение в суждение кванторных слов называется квантификацией.

2- Единичные суждения (утвердительные и отрицательные) по этой классифика­ции в особую группу не выделяются По своей характеристике они приравниваются к соответствующим общим: общеутвердительным и общеотрицательным

1Термин «Эпистемическая» происходит от греческого слова «эпистема», озна­чавшего в античной философии высший тип несомненного, достоверного знания.

1Термин «деонтическая» заимствован из греческого языка и означает «обязан­ность»

1Термин «алетический» греческого происхождения, означает «истинный»

1Софизм - логическая уловка, софист - человек, прибегающий к логической уловке

1В логическом квадрате слово «некоторые» употребляется в значении «по край­ней мере, некоторые».

1Существует другая так называемая атрибутивная формулировка: признак признака некоторой вещи есть признак самой этой вещи, то что противоречит признаку вещи, противоречит вещи.

1О распределенноcти терминов в суждениях см. гл. IV § 2. Распределенность термина обозначается знаком «+», нераспределенность - знаком «-».

1От латинского lemma - «предположение».

2От латинского alternare -«чередоваться»; каждая из двух или нескольких исключающих друг друга возможностей.

1Энтимема в переводе с греческого буквально означает «в уме»

1От греческого «куча» (куча посылок).

1Термин «доказательство» в процессуальном праве употребляется в двух смыс­лах: (1) для обозначения фактических обстоятельств, выступающих носителями ин­формации о существенных сторонах уголовного или гражданского дела (например, угроза обвиняемого в адрес потерпевшего; оставленные на месте совершения пре­ступления следы и т.д.); (2) для обозначения источников информации о фактических обстоятельствах, имеющих отношение к делу (например, показания свидетелей, пись­менные документы и т.д.).